Вращение вокруг своей оси при поднятии плеч кость. БИОМЕХАНИКА

⇐ Предыдущая Стр 2 из 11 Следующая ⇒

Биомеханика человека – это составная часть прикладных наук, изучающих движение человека.

Плоскости .

Для обозначения положений тела человека в пространстве, расположения его частей относительно друг другу используют понятия о плоскостях и осях.

Исходным принято считать такое положение тела, когда человек стоит, ноги вместе, ладони обращены вперед.

Сагиттальная плоскость разделяет правую и левую половины тела. Частным случаем сагиттальной плоскости является срединная плоскость, она проходит точно посередине тела, разделяя его на две симметричные половины. (на рис. красная, sagittal plane)

Фронтальная плоскость -отделяет переднюю часть тела от задней. Расположена вертикально и ориентирована слева направо. Перпендикулярна сагиттальной (на рис. синяя, coronal plane)

Горизонтальная плоскость - или поперечная плоскость, перпендикулярна двум первым и параллельна поверхности земли, она отделяет вышележащие отделы тела от нижележащих. (на рис. зеленая, transverse plane)

Эти три плоскости могут быть проведены через любую точку тела человека. При пересечении двух взаимно-перпендикулярных плоскостей образуется ось вращения.

Оси вращения :

Вертикальная ось – образуется при пересечении сагиттальной и фронтальной плоскостей. Направлена вдоль тела стоящего человека.

Вокруг этой оси возможны пронация, супинация, а также повороты туловища и головы.

Фронтальная ось – образуется при пересечении фронтальной и горизонтальной плоскостей. Ориентирована слева направо или справа налево. Вокруг этой оси происходит сгибание и разгибание.

Сагиттальная ось – образуется при пересечении сагиттальной и горизонтальной плоскостей. Ориентирована в переднезаднем направлении. Вокруг этой оси происходит отведение и приведение, поднимание и опускание лопаток, латеральное сгибание туловища.

Для анализа упражнений очень важно знать названия движений и понимать, в каких суставах они совершаются.

Названия движений :

Супинация-вращение наружу

Пронация-вращение внутрь

Аддукция-сведение,приведение

Абдукция-разведение, отведение

Циркумдуция-круговое вращение.

Сустав/сегмент тела	Возможные движения
позвоночник	Сагиттальная ось-латеральное сгибание\разгибание (наклоны в сторону) Фронтальная ось- сгибание\разгибание Вертикальная ось- вращение
Грудино-реберные суставы	неподвижные
Суставы головки ребер и реберно-поперечные суставы	Вращение по оси шейки ребра. Верхние рабра двигаются преимущественно вперед, нижние ребра преимущественно в стороны.

Вращение вокруг неподвижной оси. Тем. Вращения тела вокруг неподвижной оси

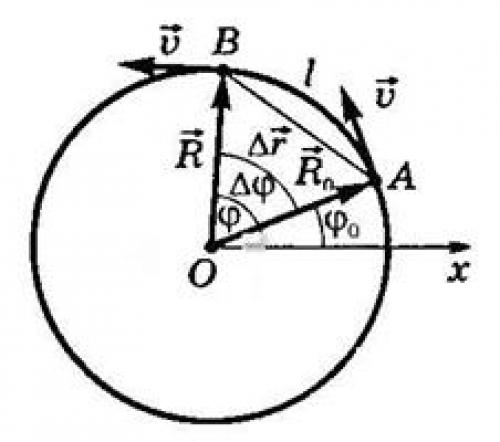
§1. Движение тела по окружности с постоянной по модулю скоростью

Движение тела по окружности с постоянной по модулю скоростью - это движение, при котором тело за любые равные промежутки времени описывает одинаковые дуги.

Положение тела на окружности определяется радиусом-вектором , проведенным из центра окружности. Модуль радиуса-вектора равен радиусу окружности R (рис. 1).

Рис.1. Движения тела по окружности

За время ∆t тело, двигаясь из точки А в точку В, совершает перемещение , равное хорде АВ, и проходит путь, равный длине дуги l .

Радиус-вектор поворачивается на угол ∆φ. Угол выражают в радианах.

Скорость движения тела по траектории (окружности) направлена по касательной к траектории. Она называется линейной скоростью. Модуль линейной скорости равен отношению длины дуги окружности l к промежутку времени ∆t, за который эта дуга пройдена:

Скалярная физическая величина, численно равная отношению угла поворота радиуса-вектора к промежутку времени, за который этот поворот произошел, называется угловой скоростью:

В СИ единицей угловой скорости является радиан в секунду .

При равномерном движении по окружности угловая скорость и модуль линейной скорости — величины постоянные: ω= const ; v= const .

Положение тела можно определить, если известен модуль радиуса- вектора и угол φ, который он составляет с осью О х (угловая координата). Если в начальный момент времени t₀=0 угловая координата равна φ₀, а в момент времени t она равна φ, то угол поворота ∆φ радиуса-вектора за время ∆t=t-t₀ равен ∆φ=φ-φ₀. Тогда из последней формулы можно получить кинематическое уравнение движения материальной точки по окружности: φ=φ ₀ +ωt

Оно позволяет определить положение тела в любой момент времени t.

Учитывая, что , получаем:

— формула связи между линейнойи угловой скоростью.

Промежуток времени Т , в течение которого тело совершает один полный оборот, называется периодом вращения: где N – число оборотов, совершенных телом за время Δt .

За время ∆t =Т тело проходит путь l =2πR. Следовательно,

Величина ϑ, обратная периоду, показывающая, сколько оборотов совершает тело за единицу времени, называется частотой вращения:

Следовательно, .

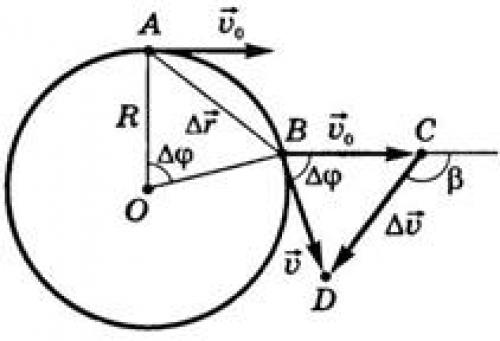
§2. Ускорение при движении тела по окружности с постоянной по модулю скоростью (центростремительное ускорение)

При равномерном вращении по окружности модуль скорости движения тела не изменяется, но направление скорости изменяется непрерывно. Следовательно, данное движение - движение с ускорением. Оно характеризует быстроту изменения скорости по направлению.

Рис.2. Равномерное движение тела по окружности

Ускорение направлено по радиусу к центру и поэтому называется центростремительным ускорением:

Модуль , направление непрерывно изменяется (рис. 3). Поэтому данное движение не является равноускоренным.

Рис.3. Направление центростремительного ускорения

§3. Вращательное движение твердого тела вокруг оси. Угловая скорость и угловое ускорение

Для кинематического описания вращательного движения абсолютно твердого тела вокруг неподвижной оси используются те же величины, что и для описания движения материальной точки по окружности.

Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение, при котором какие-нибудь две точки, принадлежащие телу (или неизменно с ним связанные), остаются во все время движения неподвижными (рис.4).

Промежуток времени, в течение которого тело совершает один полный оборот вокруг оси, — период вращения (Т) . Величина, обратная периоду, — частота вращения ( ν ) .

Проходящая через неподвижные точки А и В прямая АВ называется осью вращения.

Так как расстояния между точками твердого тела должны оставаться неизменными, то очевидно, что при вращательном движении все точки, принадлежащие оси вращения, будут неподвижны, а все остальные точки тела будут описывать окружности, плоскости которых перпендикулярны оси вращения, а центры лежат на этой оси.

Для определения положения вращающегося тела проведем через ось вращения, вдоль которой направим ось Az , полуплоскость - неподвижную и полуплоскость, врезанную в само тело и вращающуюся вместе с ним (рис. 4).

Рис.4. Вращательное движение тела

Тогда положение тела в любой момент времени однозначно определится взятым с соответствующим знаком углом φ между этими полуплоскостями, который назовем углом поворота тела. Будем считать угол φ

Уравнение выражает закон вращательного движения твердого тела вокруг неподвижной оси.

При вращательном движении абсолютно твердого тела вокруг неподвижной оси углы поворота радиуса-вектора различных точек тела одинаковы.

Основными кинематическими характеристиками вращательного движения твердого тела являются его угловая скорость ω и угловое ускорение ε.

Вращение вокруг своей оси. Как вращается Земля

Привет дорогие читатели! Сегодня хотелось бы затронуть тему Земли и Вселенной , и я подумала, что пост о том, как вращается Земля Вам пригодится Ведь от этого зависит день и ночь, а еще времена года. Давайте со всем познакомимся поближе.

Наша планета вращается вокруг своей оси и вокруг Солнца. Когда она делает один оборот вокруг оси проходит один день, а когда вокруг Солнца – один год. Далее подробнее об этом:

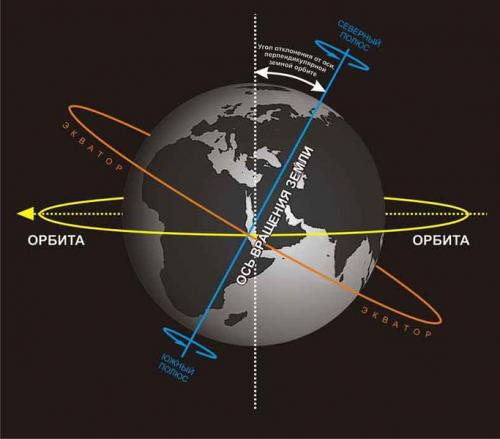
Земная ось.

Земная ось (ось вращения Земли) – это прямая, вокруг которой происходит суточное вращение Земли; эта линия проходит через центр Земли и в географических полюсах пересекает поверхность Земли.

Наклон оси вращения Земли.

Ось вращения Земли наклонена к плоскости под углом 66°33´; благодаря этому происходит изменение времен года . Когда Солнце находится над Северным тропиком (23°27´ с. ш.), в Северном полушарии начинается лето, а Земля при этом находится на самом дальнем расстоянии от Солнца.

Когда Солнце поднимается над Южным тропиком (23°27´ ю. ш.), в Южном полушарии начинается лето.

В Северном полушарии в это время начинается зима. Притяжение Луны, Солнца и других планет не изменяет угол наклона земной оси, но приводит к тому, что она перемещается по круговому конусу. Это перемещение называется прецессией.

Северный полюс в наше время направлен на Полярную звезду. Земная ось за следующие 12 000 лет, в результате прецессии, пройдет приблизительно полдороги, и будет направлена на звезду Вега.

Около 25 800 лет составляет полный цикл прецессии и существенно влияет на климатический цикл.

Два раза в год, когда Солнце находится непосредственно над экватором, и два раза в месяц, когда Луна занимает аналогичное положение, притяжение, которое обусловлено прецессией, уменьшается к нулю и происходит периодическое увеличение и снижение темпов прецессии.

Такие колебательные движения земной оси известны как нутация, которая достигает максимума каждые 18,6 лет. По значимости влияния на климат эта периодичность занимает второе место после изменения времен года .

Вращение Земли вокруг своей оси.

Суточное вращение Земли – движение Земли против часовой стрелки, или с запада на восток, если смотреть с Северного полюса мира. Вращение Земли определяет длительность дня и вызывает изменение дня и ночи.

Вокруг своей оси Земля делает один оборот за 23 часа 56 минут и 4,09 секунды. За период одного витка вокруг Солнца, Земля приблизительно совершает 365 ¼ оборотов, это составляет один год или равняется 365 ¼ суток.

Каждые четыре года в календарь добавляется еще один день, потому что на каждый такой виток, кроме целых суток, затрачивается еще четверть суток. Вращение Земли постепенно замедляет гравитационное притяжение Луны, и продлевает сутки приблизительно на 1/1000 с каждое столетие.

Судя по геологическим данным, темпы вращения Земли могли изменяться, но не более чем на 5%.

Вращение Земли вокруг Солнца.

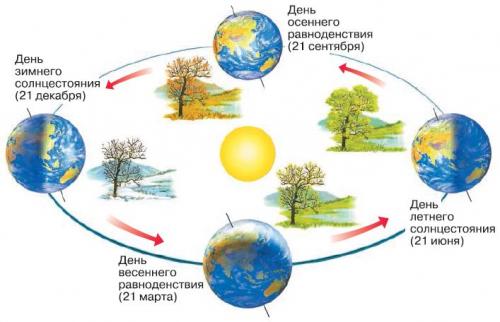
Вокруг Солнца Земля вращается по эллиптической орбите, близкой к круговой, со скоростью около 107 000 км/час в направлении с запада на восток. Среднее расстояние к Солнцу 149 598 тыс. км, а разница между самым меньшим и самым большим расстоянием 4,8 млн. км.

Эксцентриситет (отклонение от круга) земной орбиты немного изменяется на протяжении цикла длительностью 94 тыс. лет. Считается, что формированию сложного климатического цикла способствуют изменения расстояния к Солнцу, а с отдельными его этапами связаны наступление и отхождение ледников во время ледниковых периодов.

Вращение вокруг линии уровня

Стр 8 из 12 Следующая ⇒

В отличие от метода замены плоскостей проекций, вращением вокруг линии уровня плоскость общего положения в плоскость уровня можно преобразовать за одно вращение.

Сущность метода вращения вокруг линии уровня заключается в том, что плоский геометрический объект совмещается с плоскостью уровня, проходящей через ось вращения. И на соответствующую плоскость проекций плоская фигура проецируется без искажения. Каждая точка заданного геометрического объекта вращается в своей плоскости, перпендикулярной линии уровня. Траектория движения точки – окружность, центр которой находится на оси вращения, а радиус вращения равен расстоянию от точки до оси вращения.

Если за ось вращения взята горизонталь, то траектория вращения точки на горизонтальную плоскость проекцийпроецируется в виде отрезка, перпендикулярного горизонтальной проекции горизонтали. Новое положение точки будет определено, когда горизонтальная проекция траектории ее движения будет равна натуральной величине радиуса вращения.

Рис. 5.4

Рис. 5.5

Пример: Определить натуральную величину треугольника.

Рис. 5.6

Положение плоскости, при котором она становится плоскостью уровня, определяется вращением только одной ее точки, в данном случае – точки А .

Лекция 7

Вращение вокруг проецирующих прямых

Этот метод, как и метод вращения вокруг линии уровня, предполагает неизменность системы плоскостей проекций, в которой вокруг проецирующей оси вращается геометрический объект – точка, прямая или плоская фигура. При этом все точки, принадлежащие геометрическому объекту, вращаются в параллельных плоскостях, расположенных перпендикулярно оси вращения.

Вращение точки

Рис. 5.7

Траектория движения точки – окружность (дуга окружности), центр которой находится на пересечении оси вращения с плоскостью вращения, а радиус вращения равен расстоянию от точки до оси.

На КЧ траектория движения проецируется без искажения на ту плоскость проекций, к которой ось вращения перпендикулярна. На другие плоскости проекций она проецируется в виде отрезка, параллельного оси проекций.

Вращение прямой

Вращение прямой линии на КЧ сводится к вращению на один и тот же угол двух принадлежащих ей точек. Однако вращение прямой можно свести к вращению одной ее точки на заданный угол, если учитывать, что при вращении вокруг проецирующей оси проекция прямой на плоскость проекций, к которой эта ось перпендикулярна, остается равной самой себе.

Возьмем отрезок АВ , принадлежащий прямой общего положения, и повернем его вокруг фронтально-проецирующей оси j так, чтобы он стал параллелен горизонтальной плоскости проекций ( 1 основная задача ). На КЧ показана траектория вращения только одной точки, принадлежащей заданной прямой, находящейся на минимальном расстоянии от оси вращения.

Рис. 5.8

Если ось вращения на чертеже не задана, то ее можно выбрать таким образом, чтобы она пересекала прямую, тогда поворот вокруг нее значительно упрощается. На рис. 5.8 горизонтально-проецирующая ось вращения i пересекает горизонтальную прямую (A’B’) . Тогда вращением вокруг нее одного из концов отрезка прямая преобразовывается в фронтально-проецирующую прямую ( 2 основная задача ).

Вращение плоскости

Вращение плоскости вокруг проецирующей оси сводится к вращению на один и тот же угол элементов, определяющих эту плоскость в пространстве.

Возьмем плоскость общего положенияи вращением вокруг проецирующей оси преобразуем ее в проецирующую плоскость ( 3 основная задача ). Для этого преобразования необходимо провести одно вращение, при котором линия уровня плоскости превратится в проецирующую прямую.

Чтобы найти натуральную величину плоской фигуры, следует провести второе вращение, преобразовав проецирующую плоскость в плоскость уровня ( 4 основная задача ).

Вращение вокруг горизонтали. Способ вращения вокруг проецирующей прямой

Перемещение точки при её вращении вокруг проецирующей прямой является частным случаем параллельного перемещения и подчиняется следующим правилам.

Траектория движения точки – дуга окружности с центром, расположенным на оси вращения. Радиус окружности равен расстоянию между точкой и осью вращения.
При вращении точки вокруг прямой, перпендикулярной фронтальной плоскости проекции, фронтальная проекция точки перемещается по дуге окружности, а горизонтальная – параллельно оси X.
При вращении точки вокруг прямой, перпендикулярной горизонтальной плоскости проекции, горизонтальная проекция точки перемещается по дуге окружности, а фронтальная – параллельно оси X.

Руководствуясь рассмотренными правилами, повернем отрезок CD в положение, параллельное фронтальной плоскости проекции. В качестве оси вращения i будем использовать горизонтально проецирующую прямую, проведенную через точку D.

При повороте отрезка положение точки D не изменится, поскольку она лежит на оси i. Точку C' переместим по дуге окружности радиусом C'D' в положение C'₁так, чтобы выполнялось условие C'₁D'₁|| X. Для нахождения точки C''₁ из C'' проведем прямую, параллельную оси X, до пересечения её с линией связи, восстановленной из т. C'₁.

На следующем рисунке показан способ перевода отрезка в горизонтально проецирующее положение. Построения выполнены в два этапа и описаны ниже.

Сначала вращением вокруг оси i₁CD перемещают в положение C₁D₁, параллельное фронтальной плоскости проекции. После этого вращением вокруг оси i₂отрезок переводится в искомое положение C₂D₂, где он перпендикулярен горизонтальной плоскости проекции.

Расположение осей вращения выбирают исходя из удобства дальнейших построений. В нашей задаче горизонтально проецирующая прямая i₁проходит через точку D, а проекция i''₂фронтально проецирующей прямой i₂лежит на продолжении отрезка C''₁D''₁.

Вращение вокруг оси. Кэррингтоновское вращение

Кэррингтоновское вращение представляет собой систему для сопоставления положений деталей на поверхности Солнца, разделённых некоторым промежутком времени, что позволяет отслеживать эволюцию групп солнечных пятен или вспышек.

Поскольку параметры вращения Солнца меняются с широтой, глубиной слоя и со временем, то подобные системы сравнения носят приблизительный характер. В случае модели кэррингтоновского вращения период обращения Солнца принят равным 27,2753 суткам. Каждый оборот Солнца в такой схеме обладает собственным номером, началом отсчёта которого является 9 ноября 1853 года. (Число Бартельсастроится по подобной схеме, но период обращения принимается равным 27 суткам, началом отсчёта является 8 февраля 1832 года.)

Гелиографическая долгота детали на поверхности Солнца соответствует угловому расстоянию от объекта до центрального меридиана, то есть до линии от Солнца до Земли. Кэррингтоновская долгота детали является угловым расстоянием относительно фиксированной точки, положение которой указал.

Ричард Кэррингтон определил скорость вращения Солнца по данным о солнечных пятнах на низких широтах в 1850-х гг., по его оценкам сидерический период обращения Солнца равен 25,58 суток. Сидерическое вращение измеряется относительно далёких звёзд, но, поскольку Земля вращается вокруг Солнца, то для земного наблюдателя период вращения Солнца будет равен 27,2753 суток.

Можно построить диаграмму, в которой долгота пятен откладывается по горизонтальной оси, а время — по вертикальной. Долгота измеряется по времени пересечения центрального меридиана и основывается на кэррингтоновской модели вращения. Если нарисовать на такой диаграмме положение солнечных пятен после каждого оборота, то большая часть новых точек окажется строго ниже точек от предыдущих оборотов. На протяжении длительных временных интервалов возможны небольшие смещения вправо или влево.

Вращение вокруг своей оси упражнение. Тибетская гимнастика "Око возрождения": пять упражнений

Комплекс упражнений "Око возрождения" направлен на повышение энергетического уровня человека. Он основан на древних тибетских практиках, способствующих омоложению и оздоравиливанию организма.

Статьи по теме:

Тибетская гимнастика "Око возрождения": пять упражнений
Поза льва простив старения кожи
«Око возрождения»: упражнения для омоложения

первое и второе упражнения: вращение вокруг своей оси и поднятие ног

для первого упражнения необходимо встать, вытянуть перед собой руки по одной линии с плечами. затем начинайте осуществлять вращение тела по часовой стрелке, на первое время хватит и трех таких оборотов. если сильно закружилась голова, постарайтесь некоторое время удерживать взгляд на неподвижной точке. для этих целей хорошо подойдут кончики пальцев.
Для второго упражнения лягте на спину, желательно на какую-нибудь смягчающую подстилку. Руки лежат вдоль туловища, пальцы рук соединены и прижаты к полу. Поднимайте голову, прижмите подбородок к груди. Затем поднимите прямые ноги вертикально вверх, но таз постарайтесь оставить на полу. После этого вернитесь в исходную горизонтальную позицию.
При выполнении второго упражнения нужно контролировать дыхание. Находясь в горизонтальном положении, освободите свои легкие от воздуха. Поднимая голову и ноги, медленно вдохните. Опускание же головы и ног сопровождается плавным выдохом. Важно сделать акцент на глубине дыхания, сконцентрироваться на нем и на ощущениях в теле.

третье и четвертое упражнения: стоя на коленях и положение "стола"

третье упражнение выполняется стоя на коленях, причем колени расположены на ширине таза. это позволяет бедрам принять вертикальное положение. ладони нужно положить на заднюю сторону бедра, под ягодицы. подбородок прижимается к груди. далее делается следующее: голова откидывается назад и вверх, грудная клетка выставляется вперед, позвоночник прогибается назад. руки при этом могут немного упираться в бедра. опять-таки в исходном положении нужно находиться с опустошенными легкими, делать медленный вдох по мере выполнения упражнения.
Четвертое упражнение делается в положении сидя, ноги вытянуть перед собой, ступни - на ширине плеч. Спина - прямая, ладони стоят по бокам тела, пальцы соединены и смотрят вперед. Голова опускается к груди, после чего запрокидывается назад и вверх. Туловище поднимается вперед и приводится в горизонтальное положение, оно должно быть с бедрами в одной плоскости. Голени и руки служат вертикальной опорой. Постойте так несколько секунд и вернитесь в исходную позицию. Следите за дыханием на протяжении всего упражнения, начинать его стоит с пустыми легкими. Во время поднятия туловища медленно вдыхайте, в конечной точке задержите дыхание.

пятое упражнение: в позе острого угла

пятое упражнение выполняется из упора лежа, с прогнутой спиной. точками опоры служат ладони и кончики пальцев ног, остальное находится над полом. пальцы рук смотрят вперед, плотно сомкнуты. ладони и ноги поставлены на ширину плеч. голова запрокидывается назад и вверх, после чего меняем положение тела. оно по-прежнему стоит на ладонях и кончиках пальцев ног, но теперь в позе острого угла с вершиной наверху. голова прижата к груди, ноги прямые. в упоре лежа легкие пустые, при складывании тела делается вдох. в крайней точке дыхание задерживается, при возвращении в упор делается выдох.